干涉法测量是物理实验中的基本测量方法,迈克尔逊干涉仪(简称迈氏干涉仪)干涉实验就是其中一个典型实验。主要内容为观察干涉条纹及其变化,以及据此测量一些物理量。几乎所有大学物理和实验教材都只介绍干涉圆条纹和直线干涉条纹,而对椭圆和双曲线干涉条纹则避而不谈[1~3]。在实验教学中,笔者在一台迈氏干涉仪(WSM-100型,杭州光学仪器厂生产)上成功地调制出椭圆和双曲线干涉条纹。多年指导物理实验教学的实践使笔者感到现行物理实验教材中有关迈氏干涉仪产生干涉条纹的理论推导不很透彻,对学生理解实验帮助不大。而普通物理论教材中恰恰又没有这部分内容。本文从波动理论出发,对迈氏干涉仪产生各种干涉条纹的干涉机理分别用解析法、图解法进行分析并作比较。
1 解析法
图1是迈氏干涉仪的光路图,首先依次进行以下四个等效分析。
(1)激光器的平行光束通过透镜等效于一个单色点光源S;
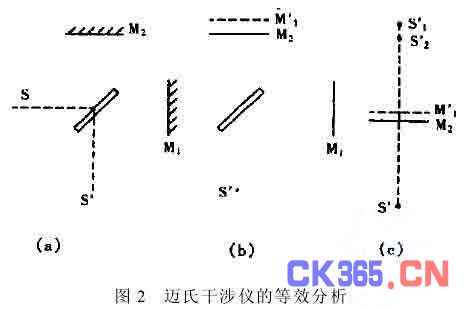
(2)点光源S在分光板G里成一虚点光源S′,见图2 (a);
(3)定镜M1在G里成一虚像M′1,见图2(b);
(4) S′在平面镜M2和M′1里成两个虚的点光源S′1和S′2,见图2 (c)。
至此,用激光照射的干涉仪等效于两个单色点光源S′1、S′2,由于两个点光源是由同一点光源S′等效过来的,当然是相干的。
两个相干点光源所产生的干涉条纹在xy平面上有相距2a的两个相干点光源S′1、S′2(如图3所示)。xy平面上任意一点P(x、y)的光强为:
至此,用激光照射的干涉仪等效于两个单色点光源S′1、S′2,由于两个点光源是由同一点光源S′等效过来的,当然是相干的。
两个相干点光源所产生的干涉条纹在xy平面上有相距2a的两个相干点光源S′1、S′2(如图3所示)。xy平面上任意一点P(x、y)的光强为:
其中I1, I2为S′1, S′2单独存在时对P点的光强贡献,ΔL则为S′1P与S′2P之间的光程差。令:ΔL=2b±nλ, n=0,1,2,…这时I(P)具有极大值。即要求: (x+a)2+y2-(x-a)2+y2=±2b ,由此计算出代表一系列亮条纹的等位相面是一组双曲线(见图3)。
其中I1, I2为S′1, S′2单独存在时对P点的光强贡献,ΔL则为S′1P与S′2P之间的光程差。令:ΔL=2b±nλ, n=0,1,2,…这时I(P)具有极大值。即要求: (x+a)2+y2-(x-a)2+y2=±2b ,由此计算出代表一系列亮条纹的等位相面是一组双曲线(见图3)。
显然,干涉场是以x轴为对称轴。因此在三维空间,等位相面是以x为轴的双曲旋转面。
显然,干涉场是以x轴为对称轴。因此在三维空间,等位相面是以x为轴的双曲旋转面。
这样一系列双曲线旋转面描述了两个点光源S′1、S′2所形成的干涉场。
在观察迈氏干涉仪干涉条纹时,往往用一屏幕(毛玻璃)放在一定位置接收,所以看到的是干涉场在一平面上的分布。现分下列几种情况讨论。
(1)圆条纹 当屏幕垂直x轴且离0点为C处(如图3位置Ⅰ),显然亮条纹是一组同心圆,其半径可由式(3)求得:
这样一系列双曲线旋转面描述了两个点光源S′1、S′2所形成的干涉场。
在观察迈氏干涉仪干涉条纹时,往往用一屏幕(毛玻璃)放在一定位置接收,所以看到的是干涉场在一平面上的分布。现分下列几种情况讨论。
(1)圆条纹 当屏幕垂直x轴且离0点为C处(如图3位置Ⅰ),显然亮条纹是一组同心圆,其半径可由式(3)求得:
如果2a为波长的整数倍,则在x轴上(即r=0)ΔL=2a应为一亮点,亮点外第m个同心圆的光程差ΔL=2b=2a-mλ,即
如果2a为波长的整数倍,则在x轴上(即r=0)ΔL=2a应为一亮点,亮点外第m个同心圆的光程差ΔL=2b=2a-mλ,即
当只考虑最高几级干涉条纹时,可以认为a m.λ2,同时考虑到c b,作近似计算,由(4)式,得出第m个圆环的半径为:
当只考虑最高几级干涉条纹时,可以认为a m.λ2,同时考虑到c b,作近似计算,由(4)式,得出第m个圆环的半径为:
由(5)式可看到,当c愈大,即屏幕愈远,而a愈小,即S′1、S′2相距愈近时,这一组同心圆的半径愈大。
(2)直线干涉条纹 当屏幕垂直y轴,且y=c处,相当于图3中Ⅱ位置,则(3)式变为:
由(5)式可看到,当c愈大,即屏幕愈远,而a愈小,即S′1、S′2相距愈近时,这一组同心圆的半径愈大。
(2)直线干涉条纹 当屏幕垂直y轴,且y=c处,相当于图3中Ⅱ位置,则(3)式变为:
显然,这是一组双曲线。假设干涉级别很小,即b=nλ2 a,则有x2b2-z2a2=c2a2,如果观察的视场很小,即z的变化范围比c小很多,则有

这是一组垂直于xy平面的等间距平行线,其间距为c2aλ
(3)椭圆和双曲线干涉条纹 如果屏幕不在图3的Ⅰ或Ⅱ位置,则屏幕上接收到的将是椭圆或双曲线干涉条纹。令屏幕的法线在xoy平面上,法线与屏幕交于x0, y0,法线与x轴成θ角,取屏幕上坐标ξ, z (见图4)。x, y坐标与ξ坐标转换关系为
![]()
将(8)式代入(3)式,得
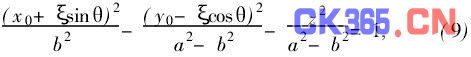
将式(9)展开后,得到ξ2项的系数为(sin2θb2-cos2θa2-b2), (9)式是ξ, z坐标上的二次曲线,当z2与ξ2的系数同号,则曲线为椭圆,现z2项的系数为负值,故椭圆条纹出现的条件
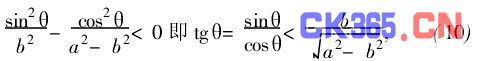
如不满足此条件,则屏幕上的干涉条纹就是双曲线。一般讲,如a一定,则θ角愈小,干涉级愈高,得到条纹常为椭圆(如图3中Ⅲ位置)。否则,则得到双曲线条纹(如图3Ⅳ位置)。
2 图解法
由上面讨论知两个相干点光源所形成的干涉场是一系列双曲线旋转面(如图5所示)。迈氏干涉仪在调整过程中,屏幕上会出现什么形状的干涉条纹,取决于M2与M′2(即S′1与S′2)的位置关系,以及屏幕与二点光源的连线成什么关系
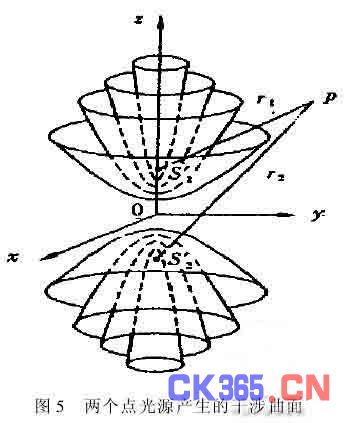
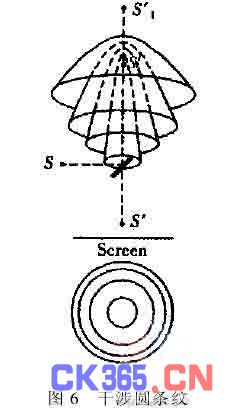
(1)如果激光束垂直定镜M1且M1垂直M2,那么屏幕与S′1S′2连线垂直,屏幕与双曲线旋转面相截的结果产生同心圆的干涉条纹,如图6所示。
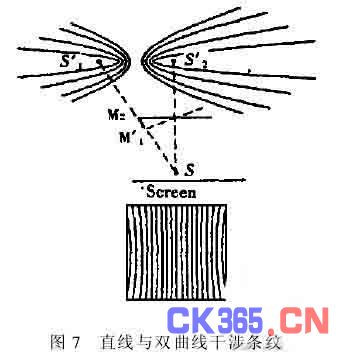
(2)如果M′1与M2相交,且有一个微小的夹角,这相当于两个对顶的空气劈尖,应该产生等厚干涉,在此情况下,由作图可见,S′1S′2的连线几乎与屏幕平行,屏幕与双曲线旋转面交线的形状为中间是直线,两边对称分布的双曲线,见图7。
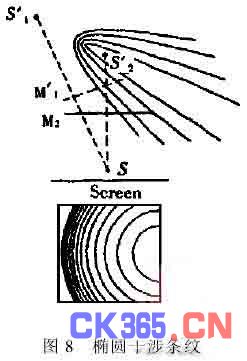
(3)如果M′1与M2不平行又不相交,那么屏幕与双曲面相截的轨迹为椭圆,见图8。
解析法是图解法的基础,很严谨,但过程不直观;图解法直观,易理解,二者结合起来相得益彰,对学生理解实验及操作仪器大有好处。
参考文献:
[1] 赵凯华,钟锡化.光学(上册) [M].北京:北京大学出版社, 1985.
[2] 孙柏忠.物理光学(上册) [M].武汉:华中理工大学出版社, 1986.
[3] 张士欣.基础物理实验[M].北京:北京科学出版社, 1997.























